勾股定律:简单却深奥的数学法则
勾股定律:简单却深奥的数学法则

大家好!今天我们来聊聊一个听起来有点严肃,但其实非常有趣的数学定理——勾股定理。它不仅是我们在学校里学到的基础知识,而且在生活中无处不在。无论你是在装修房子、玩游戏,还是在做科学实验,勾股定理都能派上用场。接下来,我会带你一起深入了解这个定理的历史、原理和应用,看看它是如何影响我们日常生活的。
一、勾股定理的历史
勾股定理的历史可以追溯到几千年前,最早的记录出现在古巴比伦,那时候的人们就已经发现了这个定理的基本概念。古巴比伦的数学家们在泥板上写下了与勾股定理相关的计算方法,虽然他们没有正式命名这个定理,但他们的研究为后来的数学发展奠定了基础。

1.1 毕达哥拉斯的贡献
不过,勾股定理的名字来源于古希腊的数学家毕达哥拉斯。毕达哥拉斯大约生活在公元前6世纪,他和他的学生们不仅研究数学,还探讨音乐和宇宙的和谐。他们认为,数学是理解世界的钥匙。毕达哥拉斯学派提出了勾股定理,指出在一个直角三角形中,斜边的平方等于两条直角边的平方之和。简单来说,就是:
\[
c^2 = a^2 + b^2
\]
这里,\(c\) 是斜边,\(a\) 和 \(b\) 是直角边。
1.2 其他文化的发现
有趣的是,其他文化也独立发现了这个定理。比如,古印度的数学家在他们的经典著作中提到过类似的关系,而中国的《周髀算经》也有关于直角三角形的描述。这说明,勾股定理是人类智慧的共同成果,不同的文化都在不同的时间发现了这个美妙的数学规律。

二、勾股定理的基本原理
2.1 定理的简单解释
勾股定理的核心内容其实很简单。想象一下一个直角三角形,它有一个直角(90度),两条直角边分别是 \(a\) 和 \(b\),斜边是 \(c\)。勾股定理告诉我们,斜边的长度是如何与直角边的长度相关的。也就是说,如果你知道了两条直角边的长度,就可以通过这个定理计算出斜边的长度,反之亦然。
2.2 证明方法
虽然勾股定理看起来很简单,但它有很多不同的证明方法。其中一种经典的证明方法是通过几何图形来实现。我们可以想象一个边长为 \(c\) 的正方形,里面放置四个直角三角形,剩下的部分会形成一个边长为 \(a+b\) 的大正方形。通过计算大正方形和四个直角三角形的面积,可以得出勾股定理的结论。这种图形化的证明方法让人觉得既直观又容易理解。

2.3 推广应用
勾股定理不仅适用于直角三角形,还可以扩展到其他几何形状。例如,在三维空间中,勾股定理可以用来计算立体图形的对角线长度。在坐标平面中,它也能帮助我们计算两点之间的距离。总之,勾股定理的应用范围非常广泛。
三、勾股定理的实际应用
3.1 建筑与工程
在建筑和工程领域,勾股定理的应用非常重要。比如,建筑师在设计房屋时,需要确保墙壁和地板是直的,很多时候他们会用到勾股定理来测量角度和长度。通过勾股定理,工程师可以计算出斜坡的长度、屋顶的高度等,确保建筑物的安全和稳定。

3.2 计算机科学
在计算机科学中,勾股定理也有广泛的应用。比如,在游戏开发中,程序员需要计算角色与物体之间的距离,以确定是否发生碰撞。通过勾股定理,他们可以快速而准确地计算出两点之间的距离,从而实现更为流畅的游戏体验。
3.3 物理学
在物理学中,勾股定理同样发挥着重要作用。比如,在研究物体的运动时,物理学家需要计算物体在不同方向上的位移。通过勾股定理,他们能够更好地理解和预测物体的运动状态。这对于理解力学、运动学等领域非常关键。

3.4 日常生活中的应用
其实,勾股定理在我们的日常生活中也随处可见。比如,当你在家里挂画时,如果想要确保画是水平的,可以用到勾股定理。你可以测量画的高度和宽度,然后计算出从墙壁到画框的距离,确保它挂得正好。
四、勾股定理的教育意义
勾股定理不仅是数学中的一个重要定理,它在教育中也占据着重要地位。学习勾股定理可以帮助学生建立几何直观,培养逻辑思维能力。通过解决与勾股定理相关的问题,学生能够锻炼自己的数学能力,为后续的学习打下坚实的基础。
4.1 培养逻辑思维
在学习勾股定理的过程中,学生需要进行逻辑推理和问题解决,这有助于培养他们的逻辑思维能力。这种能力不仅在数学学习中重要,在生活的各个方面都能发挥作用。
4.2 激发兴趣
勾股定理的应用非常广泛,学习这个定理可以激发学生对数学的兴趣。当他们发现自己在日常生活中也能用到这些数学知识时,学习的动力就会增强。

结论
勾股定理是一个简单却深奥的数学法则,它不仅在历史上有着重要地位,而且在现代生活中依然发挥着巨大的作用。从建筑工程到计算机科学,从物理学到日常生活,勾股定理无处不在,帮助我们更好地理解和解决问题。
希望通过今天的分享,大家能对勾股定理有一个更深入的了解。它不仅是数学中的一个基本概念,更是我们生活中不可或缺的工具。下次当你遇到与直角三角形相关的问题时,别忘了运用勾股定理哦!感谢大家的阅读,我们下次再见!
-

- 成都富士康做到了!从2000底薪到2300足足用了十一年!
-
2025-07-29 07:54:09
-

- 「于承惠」永远的银幕大师 名动世界的双手剑法
-
2025-07-29 07:51:54
-

- 香港最强悍匪张子强:绑架李泽钜得到10亿赎金,终被国家判处死刑
-
2025-07-29 07:49:39
-

- 小说:黑客女王重生成高三学渣,把前世认识的杀手骂得狗血淋头
-
2025-07-29 07:47:24
-

- 历史今日:荷兰东印度公司成立
-
2025-07-29 07:45:09
-

- 小太宗李忱,低调做人高调做事,为唐朝续命的好皇帝
-
2025-07-29 07:42:54
-
- 卖国贼刘连昆:建国以来最大间谍案,两岸同时拥有少将军衔
-
2025-07-29 07:40:39
-

- 回忆杀!那些年香港经典赌片,周润发周星驰刘德华
-
2025-07-29 07:38:24
-

- 《大宅门》你根本不知,白玉芬是如何让公公对杨九红放手的
-
2025-07-29 07:36:09
-

- 台湾往事:民进党是如何崛起,并成为台湾第一大党的?
-
2025-07-29 07:33:54
-

- 黄道十二宫其实不止十二个星座,副位星座也有机会成为黄金圣斗士
-
2025-07-29 07:31:39
-
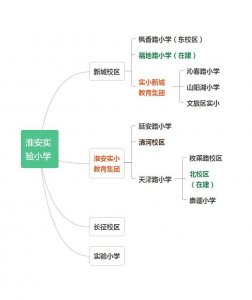
- 淮安市实验小学,长征校区,新城校区全面介绍
-
2025-07-29 07:29:24
-

- 韩三平到底什么背景?为何他的名字频繁出现在众多电影的片头?
-
2025-07-29 07:27:09
-

- 北京户口值多少钱? | 二发涨姿势
-
2025-07-29 07:24:55
-

- 25年后再看宋丹丹,承认婚内出轨却另有隐情?英达的心机令人震惊
-
2025-07-29 07:22:39
-

- 权谋横行:揭秘东汉末年黑暗时代的十常侍
-
2025-07-29 07:20:25
-

- 陈情令:为何蓝忘机对魏无羡如此深情?夷陵老祖这些魅力太耀眼
-
2025-07-29 07:18:10
-

- 一篇文章读懂印度与巴基斯坦之间的恩怨情仇
-
2025-07-28 11:01:10
-

- 110宣传日,“郑州警民通”上线,功能逆天!
-
2025-07-28 10:58:55
-

- 为什么过去人们把去东北谋生称为“闯关东”?
-
2025-07-28 10:56:40


 牛蒡是牛的什么器官(牛杂中牛蒡是牛的什么器官)
牛蒡是牛的什么器官(牛杂中牛蒡是牛的什么器官) 马晓磊同志任淄博市委书记 马晓磊简历
马晓磊同志任淄博市委书记 马晓磊简历