克莱因瓶是个啥?为什么说三维空间里无法造出真正的克莱因瓶?
克莱因瓶是个啥?为什么说三维空间里无法造出真正的克莱因瓶?
一个完全封闭的瓶子是有内外之分的,按常理来讲,如果一个物体要从封闭的瓶子内部出来(或从外面进去),都必须要穿过瓶子的表面才可以。

然而在1882年的时候,数学家菲立克斯·克莱因(Felix Christian Klein)却提出了一种奇特瓶子——克莱因瓶(Klein Bottle),简单来讲,这种瓶子没有内外之分,它可以允许物体不需要穿过瓶子的表面就能够直接从瓶子的内部出来(或从外面进去)。
克莱因瓶是个啥?
想象一下,现在有一张纸条,纸条上还有一个二维生物,对于这个二维生物来讲,这张纸条是有正反两面的,如果纸条是平的,那么这个二维生物想要从纸条的正面来到反面(或从反面来到正面),就必须要绕过纸条的边缘,或者直接穿过纸条才可以。

如上图所示,假如我们将纸条卷起来,接着将纸条的一端扭转180度,然后将纸条的两端粘在一起,这样就形成了一个没有正反面之分的二维环状结构,也就是说,在这个环状结构中,二维生物不需要绕过纸条的边缘,也不需要穿过纸条,就可以到达该结构表面上的任意一点(如下图所示)。

这种具有单侧曲面的二维环状结构由数学家奥古斯特·莫比乌斯(August Ferdinand Mobius)于1858年提出,所以人们将其称为莫比乌斯带(Mobius Band)。顺便讲一下,由于莫比乌斯带只有一个面,因此人们常将动力机械中的皮带做成这种形状,这样就可以皮带就不会只是磨损一面了。
很明显,莫比乌斯带是有边缘的,现在想象一下,假如我们取两个莫比乌斯带,然后再使用双面带将它们的边缘完全连接起来,会发生什么?

假如我们真的能够这样做,那么我们就可以得到一个封闭的结构(如上图所示)而由于莫比乌斯带是没有正反面之分的,因此我们得到的这个封闭结构也就没有内外之分,这就意味着,一个物体可以在无需穿过这个结构表面的情况下,直接从其内部出来(或从外面进去),就像下图这样。
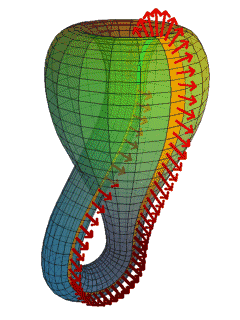
是的,这种封闭结构就是一个克莱因瓶,它其实就是莫比乌斯带在更高维度的拓展,那么这是否就意味着我们能够造出克莱因瓶呢?答案是否定的,因为在我们所在的三维空间里,根本就无法造出一个真正的克莱因瓶。
为什么说三维空间里无法造出真正的克莱因瓶?
在克莱因瓶这个概念提出之后,很多人都对这种不分内外的瓶子产生了浓厚的兴趣,人们根据其原理,还造出了像模像样的“仿克莱因瓶”,例如下图这种瓶子。

可以看到,这种“仿克莱因瓶”,虽然看上去似乎可以在无需穿过瓶子表面的情况下从其内部出来(或从外面进去),但实际上,它们瓶颈与瓶身却是相交的,也就是说,这种瓶子其实是“自己穿过了自己的表面”,而真正的克莱因瓶却不是这样子的。
实际上,这其实就是维度的限制,我们再来想象一下,在一个二维的平面中,假设有一条直线将这个平面分为了两个区域,然后这两个区域中各自都有一个点(A和B)。

如上图所示,如果我们想在这个二维的平面中将A点和B点连接起来,就必然会穿过中间的那一条直线,那有没有办法不穿过那条直线而将A点和B点连接起来呢?当然有办法,我们只需要将这个二维平面卷起来就可以“跳”过那条直线。
同样的道理,想要在三维空间中将两个莫比乌斯带的边缘完全连接起来,就必然会穿过莫比乌斯带的表面,正是因为如此,三维空间里才无法造出真正的克莱因瓶,只有在更高维度的空间中,我们才可以“跳”过莫比乌斯带的表面,直接两个莫比乌斯带连接起来,进而造出真正的克莱因瓶。
结语
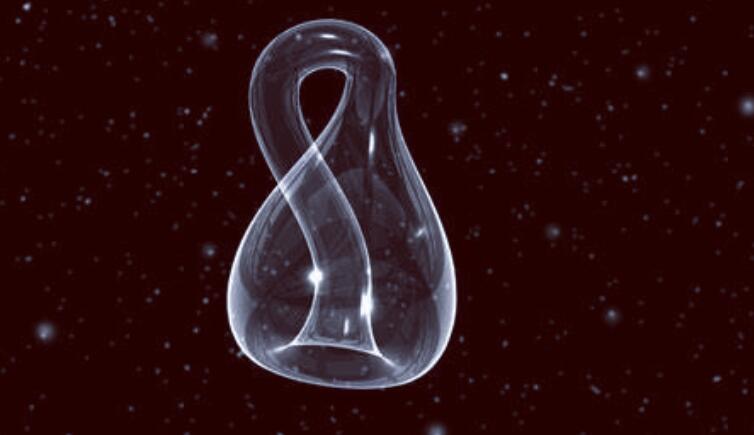
人类之所以能够建立辉煌的文明,有一个重要的原因就是人类的想象力,这种独特的能力可以让人类根据已知的现象,想象出现实世界里不存在的事物,从而使人类具备了强大的创造力。克莱因瓶其实就是人类思考高维空间时想象出来的事物,它是否能够造出并不是很重要,重要的是人类能够想到,或许在不远的未来,人类真的能够揭开高维空间的奥秘。
好了,今天我们就先讲到这里,欢迎大家关注我们,我们下次再见。
(本文部分图片来自网络,如有侵权请与作者联系删除)
-

- 绿尾大蚕蛾饲养日记:红配绿的虫宝
-
2025-10-16 21:56:03
-

- 河北这些地方不仅有玻璃栈道,更有好玩的玻璃漂流!
-
2025-10-16 21:53:48
-

- 中国最有名的词曲作家(中国作词作曲排行)
-
2025-10-16 21:51:33
-
- 什么样的女人容易出轨(女人结婚以后为什么会出轨)
-
2025-10-16 21:49:18
-

- 乔峰是洪七公的师傅吗(乔峰的降龙十八掌和洪七公)
-
2025-10-16 21:47:05
-

- 撩女孩子的套路100句,一问一答,轻松搞定她!
-
2025-10-16 21:44:48
-

- 中国历史上哪个皇帝的妃子最多(历史上妃子最多的皇帝有多少个妃子)
-
2025-10-16 21:42:32
-
- 仪式感意思是什么(大家热衷谈论的仪式感究竟是什么)
-
2025-10-16 21:40:18
-

- 食物不咸不代表没盐(对于盐是该多吃还是少吃?)
-
2025-10-16 21:38:03
-
- 55幅科幻绘画作品分享—必须收藏,科幻画大全让科学插上艺术翅膀
-
2025-10-16 07:14:24
-

- 滑轮组中关于有用功、额外功、总功以及机械效率计算全攻略
-
2025-10-16 07:12:09
-

- 简评《伪装者》小人物-于曼丽的悲惨人生
-
2025-10-16 07:09:55
-

- 高地猫是什么品种图片(高地折耳猫的性格及特点)
-
2025-10-16 07:07:40
-

- MJ之女帕丽斯·杰克逊亮相音乐杂志封面,模特歌手身份两不误
-
2025-10-15 17:59:45
-

- 中国将在南极建立首个永久机场 其难度不亚于建考察站
-
2025-10-15 17:57:30
-

- 苏轼与佛印的故事,牛粪与佛
-
2025-10-15 17:55:15
-

- 是不是馋了,今天教你做小肉饼,外皮酥脆,里面软乎,肉馅鲜香
-
2025-10-15 17:53:00
-
- 华为P20售价曝光 与预期价格相差不大
-
2025-10-15 17:50:45
-

- 海底捞宣布开放加盟:要求加盟商实力雄厚 新店投入成本800-1000万
-
2025-10-15 17:48:30
-

- 孩子过早入学好吗?孩子是否应该晚一年入学?
-
2025-10-15 17:46:15


 牛蒡是牛的什么器官(牛杂中牛蒡是牛的什么器官)
牛蒡是牛的什么器官(牛杂中牛蒡是牛的什么器官) 马晓磊同志任淄博市委书记 马晓磊简历
马晓磊同志任淄博市委书记 马晓磊简历