避开捷径,着重三阶幻方规律的多方运用
避开捷径,着重三阶幻方规律的多方运用
#夏日生活打卡季#
如图一,在九宫中,填入大于6的非连续的偶数。使其横、竖、斜向三数之和都等于66。
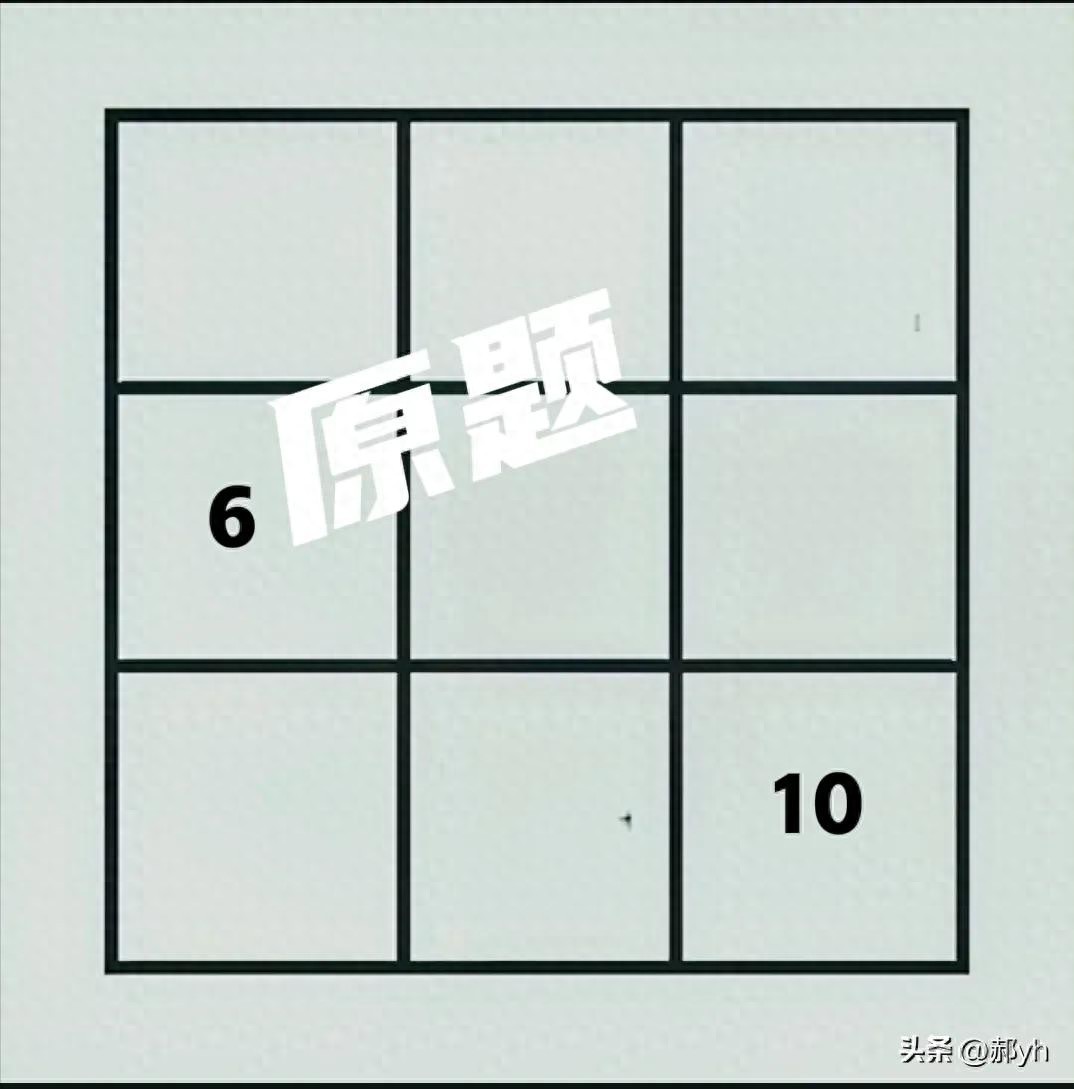
图一
解析如下:
解这类题,求中间数是关键。那么,幻和已知,中间数也就明了。实际上这题也就迎刃而解了。
但是,在此避开捷径,而着重三阶幻方规律的多方运用,以强化解题技能。
一、求中间数
1、在三阶幻方中,一共有4条过中宫(中间数)的线段,如图二,每条线上的三数之和都相等,其和称为幻和。
即:4x幻和=全体宫格数之和+3×中心(宫格)数
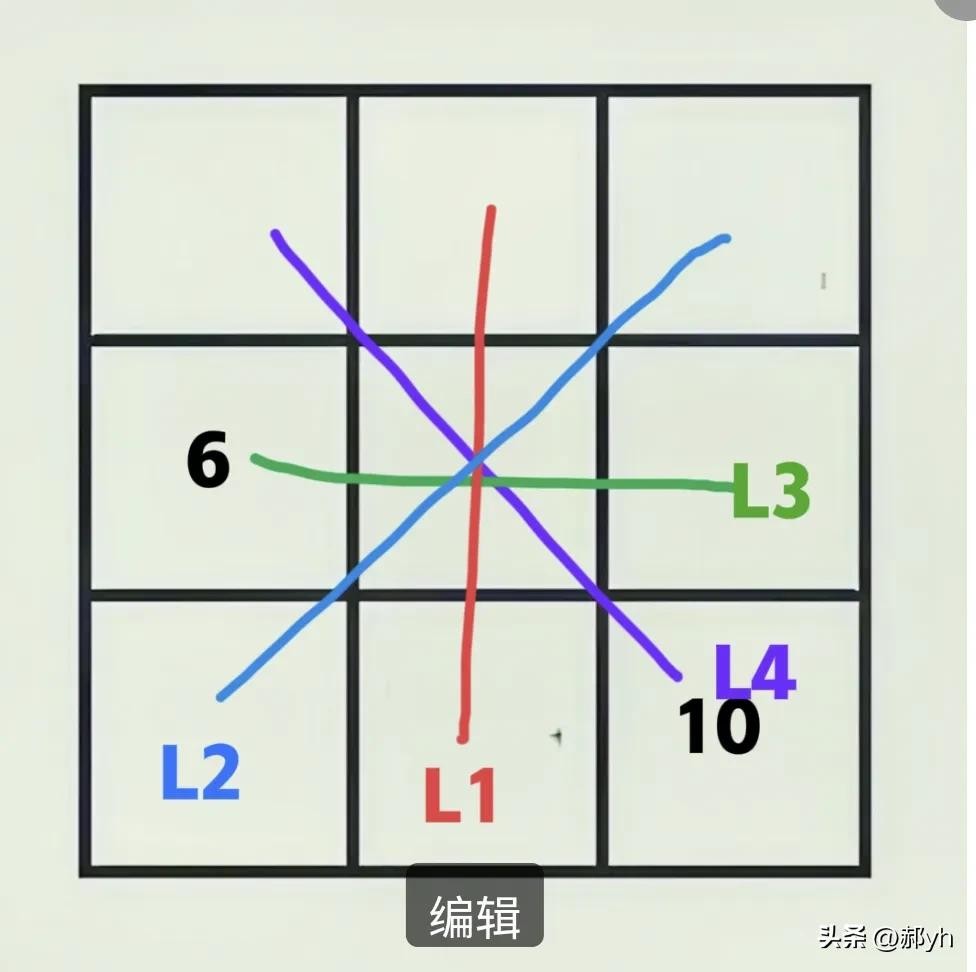
图二
2、全体宫格数之和,如图三。等于L1、L2、L3之和。即3倍的幻和
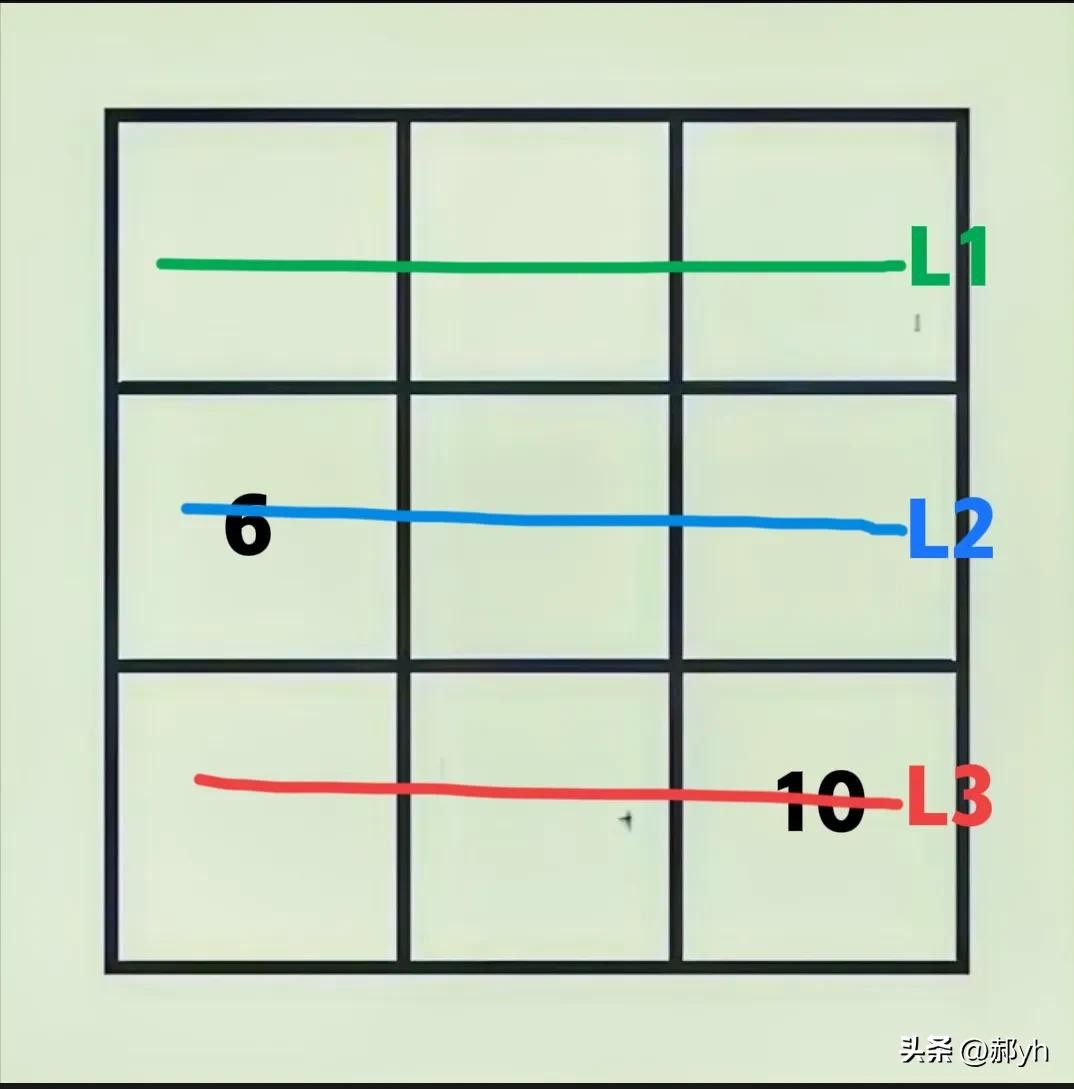
图三
综上两点,有
4×幻和=3×幻和+3×中宫数
即:幻和=3×中宫数
中宫数也就是通常所说的中间数。
换言之 中间数=幻和÷3
那么,中间数=66÷3=22
二、如图四,过左上角a有三条线,且每条线的和相等。
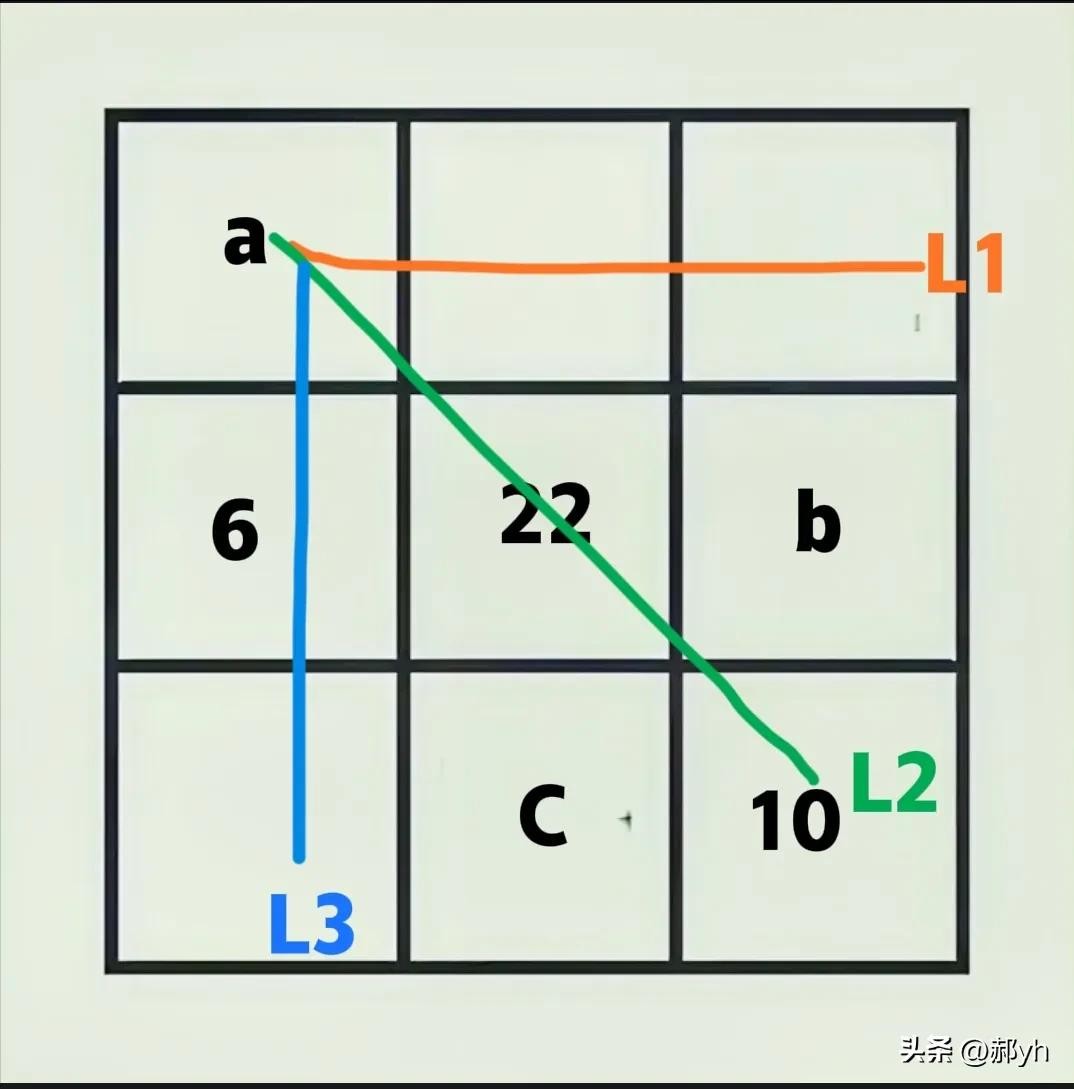
图四
全体宫格数之和=3线段之和一2a+b+c
而三线段之和即三倍幻和
所以2a=b+c
即2倍的顶角等于两底角之和,换言之:2倍角宫(格)之数等于不相邻的两边格之和,也就是三阶幻方的金三角原理。
按照这一原理,如图五。有
上边格=2×10一6=14
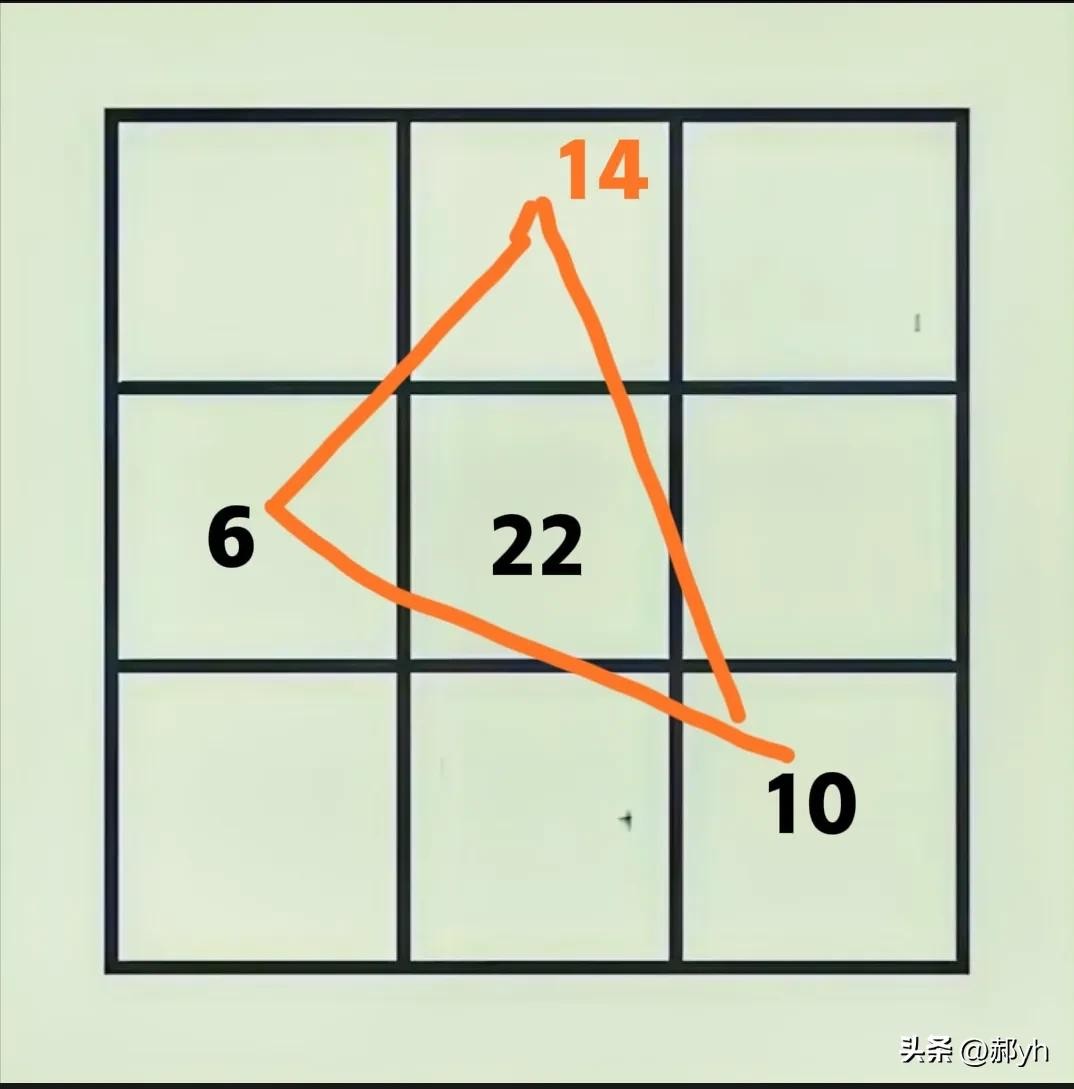
图五
三、两条线相交于公共点(可以是未知数)。
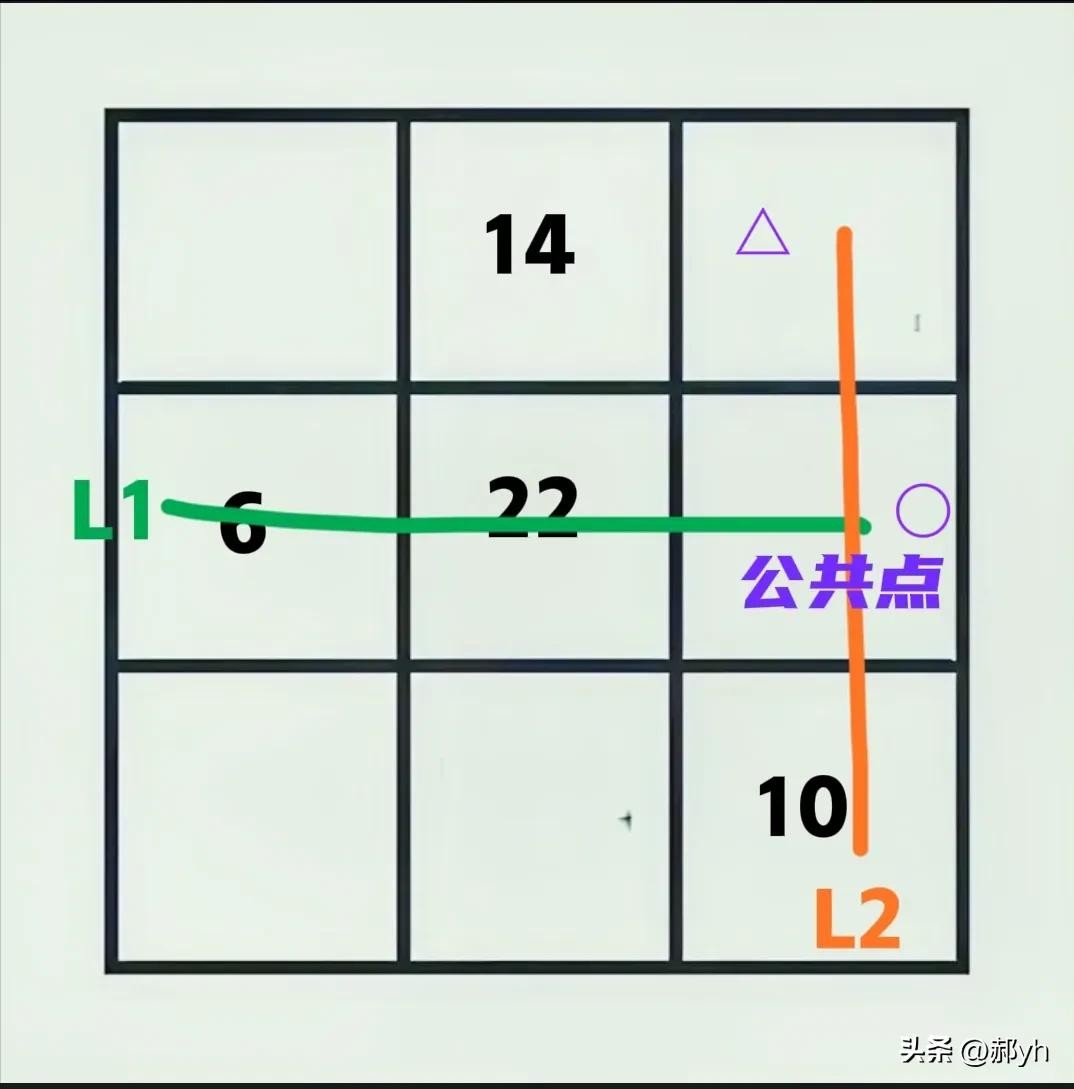
图六
1、如图六,两条线三数和(幻和)相等,
即 6+22+○=△+○+10
△(右上角)=6+22一10=18
2、如图七,两条线的和相等。
14+22+□=◇+□+10
◇=14+22一10=26
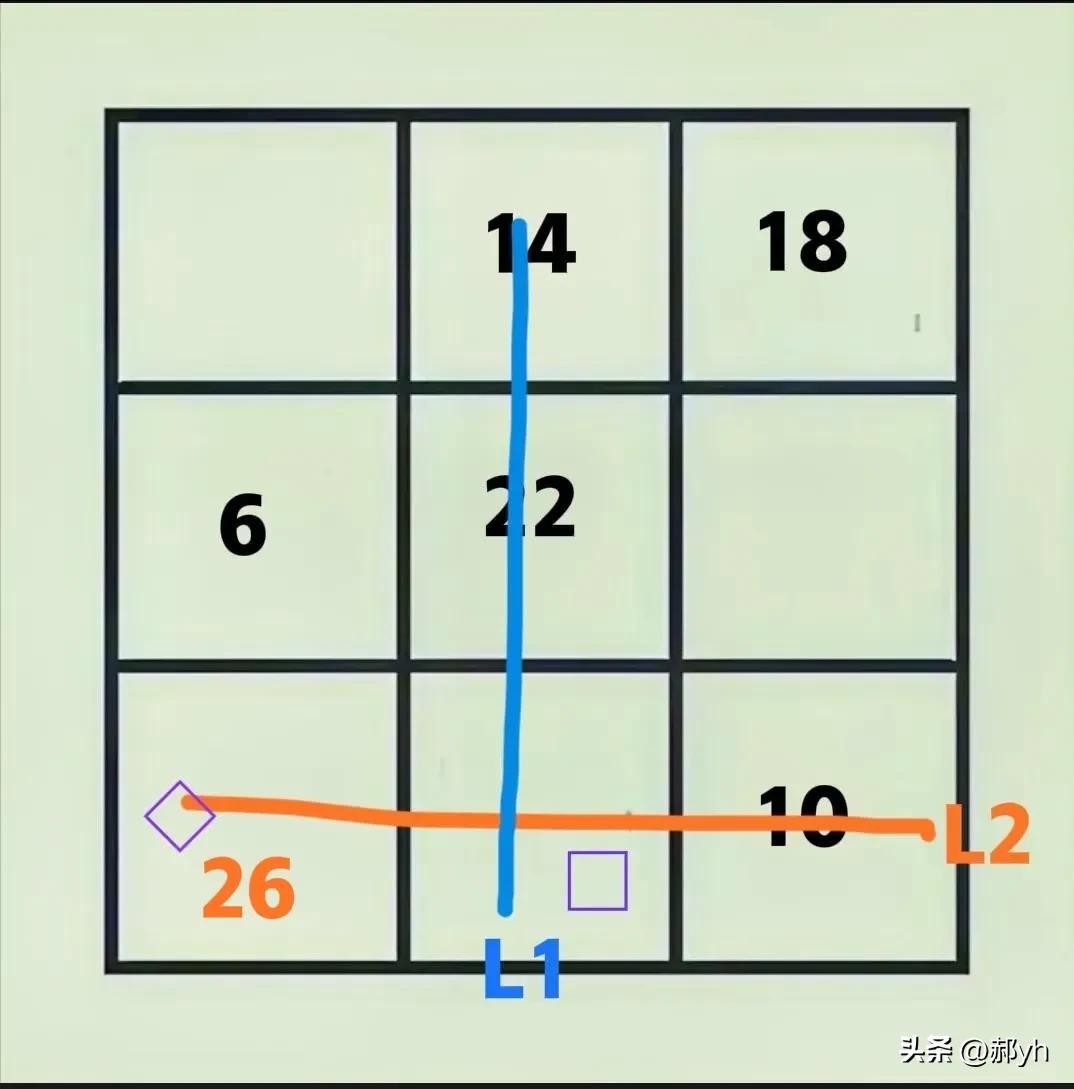
图七
四、继续运用金三角原理,如图八。
1、2×26=14+d
d(右边格)=2×26一14=38
2、2×18=6+e
e(下边格)=2×18一6=30
3、2f=38+30
f(左上角)=(38+30)÷2=34
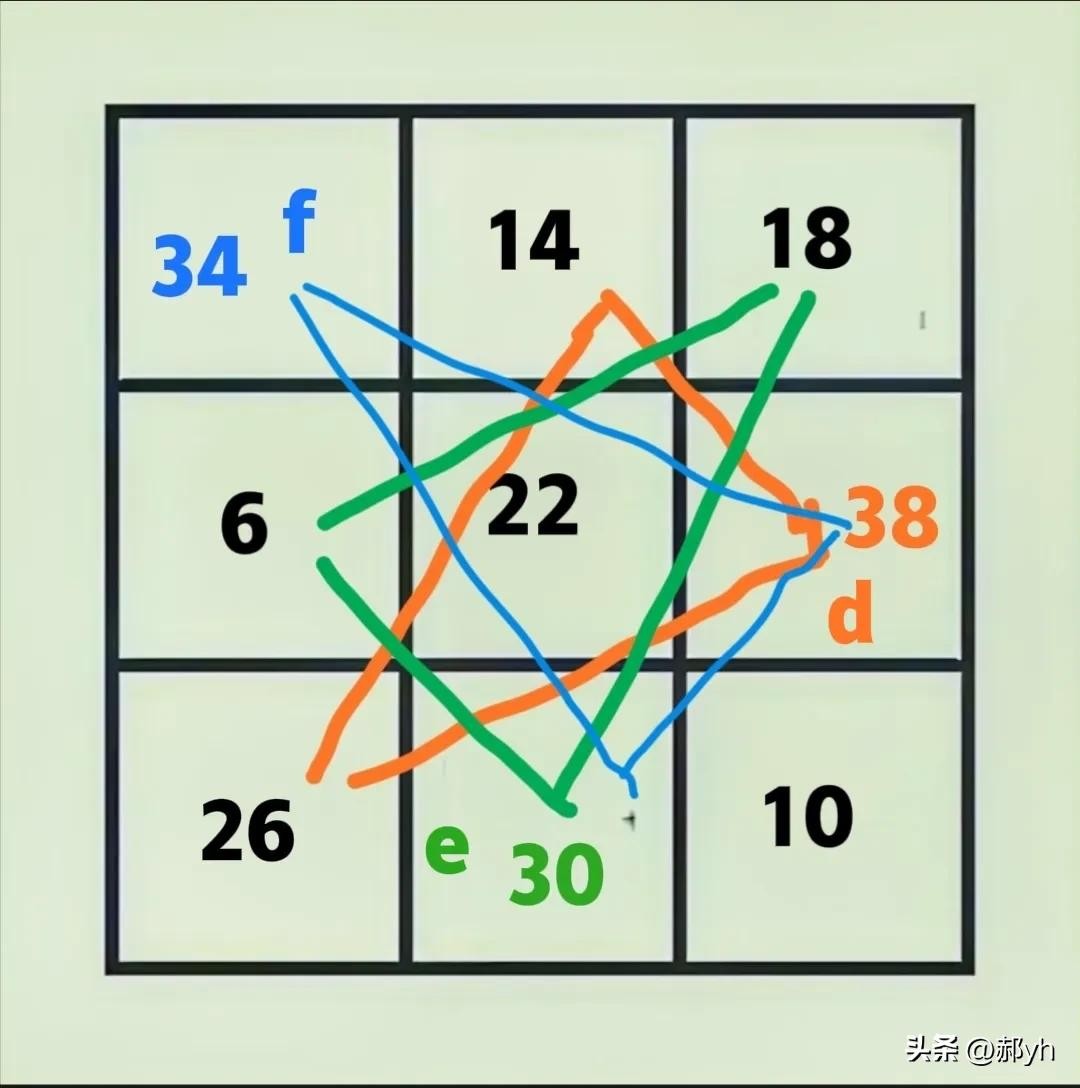
图八
到此,如图八,即为所求。
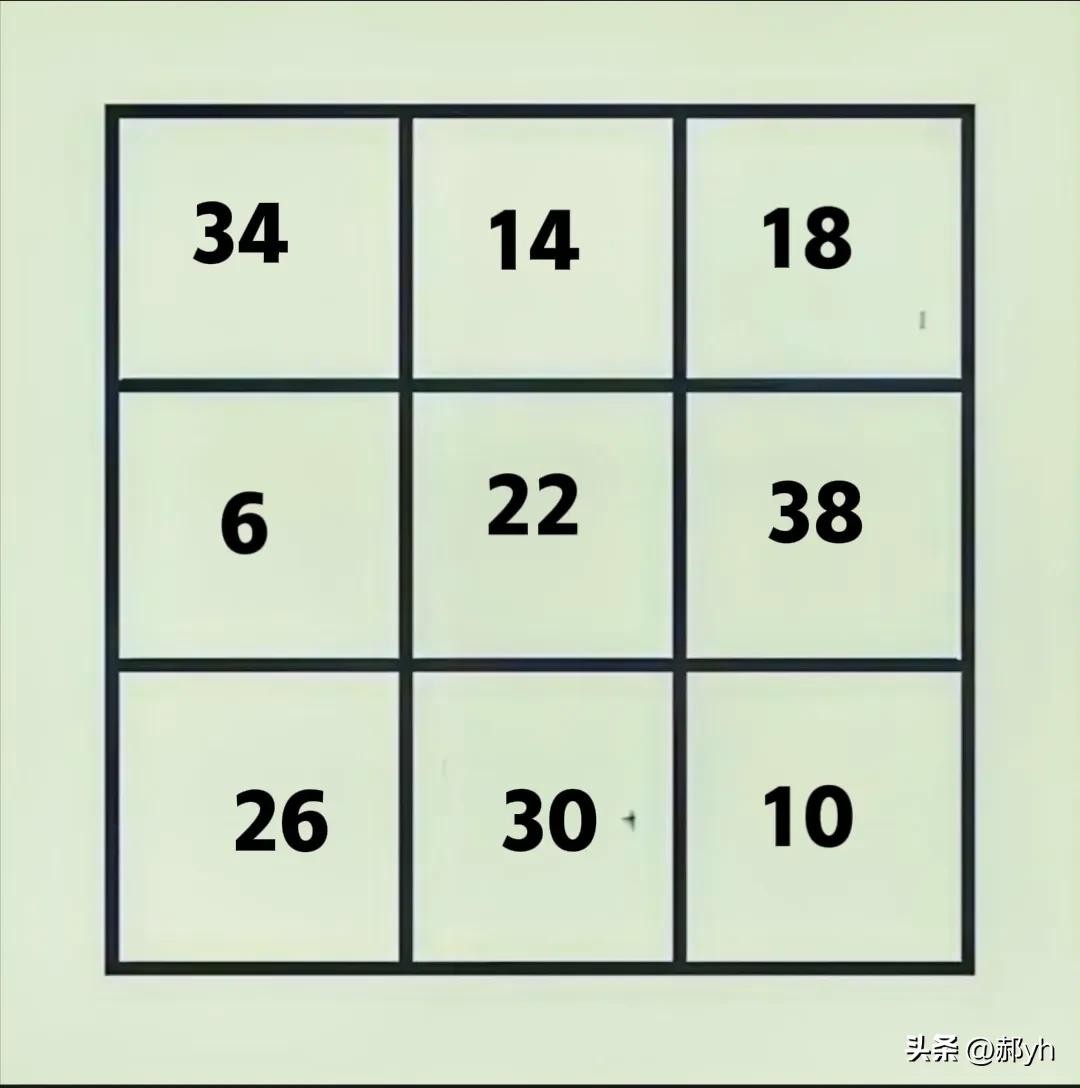
图八
经验证,每一横行、竖列、对角线的三数之和都等于66。
-

- 汤普森冲锋枪——战争史上的奇迹
-
2025-08-28 00:48:31
-

- 慈禧太后的一生
-
2025-08-28 00:46:16
-

- 陈百强励志的《摘星》,其实是一首禁毒歌曲
-
2025-08-28 00:44:01
-

- 昨日,李景亮终于杀入UFC官方排名,成该级别亚洲一哥
-
2025-08-28 00:41:46
-
- 太平良相——王旦
-
2025-08-28 00:39:31
-

- 吉祥三宝,父亲离世女儿远嫁,母亲坚守传承音乐文化,让人心疼
-
2025-08-28 00:37:16
-

- 关悦晒生日全家福,一家五口好幸福!俩女儿清秀甜美比妈妈高!
-
2025-08-28 00:35:01
-

- 歌声甜美,堪称经典听哭了《无奈的思绪》
-
2025-08-28 00:32:46
-

- 碧桂园杨惠妍、金地董事长凌克,均已正式官宣辞职
-
2025-08-28 00:30:31
-

- 66岁“黄药师”骆应钧,曾拒绝妻子生娃要求,30年享受丁克生活
-
2025-08-28 00:28:16
-

- “空姐”英语怎么说?真的不是“Air sister”
-
2025-08-28 00:26:00
-

- 世界防治结核病日:全民参与 终结结核
-
2025-08-28 00:23:45
-

- 全屋定制比木工打柜子贵多少?
-
2025-08-28 00:21:30
-
- 清远—桃花湖
-
2025-08-28 00:19:15
-
- 盘古大观:从龙头被拆到龙身被拍,北京地标建筑的命运变迁
-
2025-08-28 00:17:00
-

- 过年回家带啥上海特产?当地人推荐这些,好吃不贵,多数人没吃过
-
2025-08-27 08:05:42
-

- NBA历史最著名的五大水货状元
-
2025-08-27 08:03:27
-
- 腿长颜值低?《爱上超模》冠军Kiki康倩雯扮嫩上节目遭吐槽~
-
2025-08-27 08:01:12
-

- 26年前,邓丽君在泰国过世,与她订婚的男友保罗,如今怎样了?
-
2025-08-27 07:58:57
-

- 七月十四,鬼放肆!晚上8点前要回家?又是忌日、执日,很不一般
-
2025-08-27 07:56:42


 牛蒡是牛的什么器官(牛杂中牛蒡是牛的什么器官)
牛蒡是牛的什么器官(牛杂中牛蒡是牛的什么器官) 马晓磊同志任淄博市委书记 马晓磊简历
马晓磊同志任淄博市委书记 马晓磊简历