​中小学生掌握17个心算技巧，10倍速提升，轻松变身数学小高手！

中小学生掌握17个心算技巧，10倍速提升，轻松变身数学小高手！

心算，开启数学思维的闪电战！

心算，这个看似简单实则深藏不露的数学技能，就像是一场思维的闪电战。它不仅仅是一种计算方式，更是一种洞察数字结构、灵活运用数学规律的智慧展现。

当你面对一道复杂的计算题时，心算派的高手们能够迅速看透数字的奥秘，运用十进制、交换位置、结合率等技巧，在脑海中迅速构建出多种解题路径。他们就像是在数字的海洋中自由穿梭的潜水员，能够迅速捕捉到最精准的答案。

相比之下，笔算虽然稳妥，但往往显得过于按部就班。它需要你一步步来，每个数字都得仔细算上几遍，才能得出最终的答案。而心算则能让你在瞬间捕捉到数字之间的关联，迅速得出答案，大大节省了时间和精力。

那么，你是不是也被心算的魅力所吸引了呢？它不仅能够锻炼你的数学思维，还能让你在面对复杂问题时更加从容不迫。快来一起探索心算的奥秘吧，让你的数学思维也来一次闪电般的提升！

01 如何计算79+47——心算有多种运算方法

加法，不只是简单的数字堆砌，它是一门艺术，一门心算的艺术！

方法一：分步加法，轻松上手

先将79与40相加，脑海中浮现79，加上40，个位数不变，仍是9！70+40=110，再加上个位的9+7（先算9+6=15，再+1=16），得到126！

方法二：十位先行，大局在握

十位数相加，70+40=110，快速锁定大体数值！个位数9+7=16，完美收尾，110+16=126！

方法三：巧借巧还，速算无敌

将79看作80-1，与47相加后再减1，127-1=126，心算小能手就是你！或者，从47里借1给79，46+80=126，借来还去，轻松搞定！

✨ 心算达人秘籍 ✨

尝试多种方法，找到最适合你的那一种！经常练习，避免粗心大意，让错误无处遁形！

心算，让计算变得简单又有趣！快来一起成为心算小达人吧！

02 如何计算589+762——交换律·结合律

三位数相加，轻松搞定！

面对三位数相加，你是否又开始头疼？别怕，我们有一个简单又实用的方法！

拆分法，让计算变得简单

将三位数拆分成整百、整十和个位，比如589=500+80+9，762=700+60+2。这样，我们就可以随意排序、相加，让计算变得更灵活！

多种思路，任你选

顺序相加：589+700=1289，再加60=1349，最后加2=1351。简单明了，一步步来！分组相加：先算500+700=1200，再算80+60=140，最后9+2=11。三组数相加，答案依然准确！部分相加后组合：58+76=134，末尾添0变1340；再算9+2=11，最后1340+11=1351。这个方法也很巧妙哦！

小技巧：答案验证

得出答案后，别忘了检查个位数。比如这道题，答案的个位数只能是1（因为9+2=11）。如果答案是个位数是其他数字，那就说明计算过程中可能有误哦！

选择你喜欢的方法

我们每个人都有自己喜欢的计算方式。在计算三位数相加时，你可以从上面的方法中挑选最适合自己的两种来计算。只要答案一致，你就可以放心啦！

快来试试吧！用我们的方法，三位数相加也能变得轻松又愉快！

03 如何计算398+567——10的整倍数

十进制计算小窍门，让数学变得超简单！

十进制基础，轻松掌握！

我们的计算都离不开十进制。当数字大于10时，就向前一位进一，这个规则简单又实用！

整倍数计算，秒出结果！

遇到10、100、1000这样的整倍数，计算瞬间变得超简单！比如1000+356，张口就来1356！

棘手数字？不存在的！

像637这样的数字有点尴尬，但700就好算多了。398和567也是棘手货？别急，398离400就差一点点，先算400+567=967，再减去多加的2，答案965轻松get！

运用整倍数，计算飞起来！

在十进制里，用整倍数来计算，速度飞快！比如99+298+197，先算100+300+200=600，再减去多加的6，答案594秒出！

九九乘法小窍门！

学习九九乘法口诀时，有个小窍门哦！9，18，27...81，这些数字的个位数是按照9、8、7...1的顺序依次减1排序的。掌握了这个小技巧，乘法口诀记得更牢！

快来试试这些十进制计算小窍门吧，让你的数学之路畅通无阻！

04 如何计算1000-632——找零计算法

收银员必备！找零计算大法，轻松get！

在那个收银机还没普及的年代，店员们的找零计算能力可都是杠杠的！今天，我们就来揭秘三种超实用的找零计算方法，任你挑选，喜欢哪种就用哪种！

方法一：999减法大法

将1000-632看作999-632，无需退位，简单快捷！999-632=367，再加1，答案就是368！

方法二：9-9-10法则

将1000看作990和10，分别进行减法运算！百位9-6=3，十位9-3=6，个位10-2=8，答案368轻松得出！孩子们都爱称它为“9-9-10法则”，记得超快哦！

方法三：逆向思维加法

思考一下，632还需要多少才能到1000呢？这就是我们的逆向思维加法！632加300，百位就到9了；再加60，十位也到9了；这样就有360了。最后加8，答案就是368！参照图示，一目了然！

这种“找零计算法”不仅适用于1000-632，还适用于其他情况哦！比如800-347，先用百位数的3加400，再用十位数的4加50，最后用个位数的7加3，答案就是453！

快来试试这些找零计算方法吧，让你的计算能力瞬间提升，成为生活中的小能手！

05 如何计算1316-598——多减去一点

“10的整倍数”减法绝招，让你秒变数学高手！

在减法中，“10的整倍数”简直就是神器！之前我们练习了被减数为整数的减法，现在来看看减数接近整数时该怎么办！

以1316-598为例，如果减数是600，那该多简单啊！

没错！我们就是要故意把598当作600来算！

故意多减：1316-600，一下子就得出716！但别急，这只是个中间步骤，因为我们多减了2。还回多减的数：把多减的2还回来，716+2=718！搞定！原题1316-598的答案就是718！

思路梳理：

遇到减数接近整数时，先故意把它当作整数来算。算完后，把多减或少减的数还回来，就得到正确答案了！

想象一下：

手里有1316颗小弹珠，交给老师598颗。不如先交600颗，再让老师还你2颗，是不是一样方便呢？

快来试试这个绝招吧！让你的减法计算变得飞快又准确！

那么，用算式写出来是怎样的呢？请看：

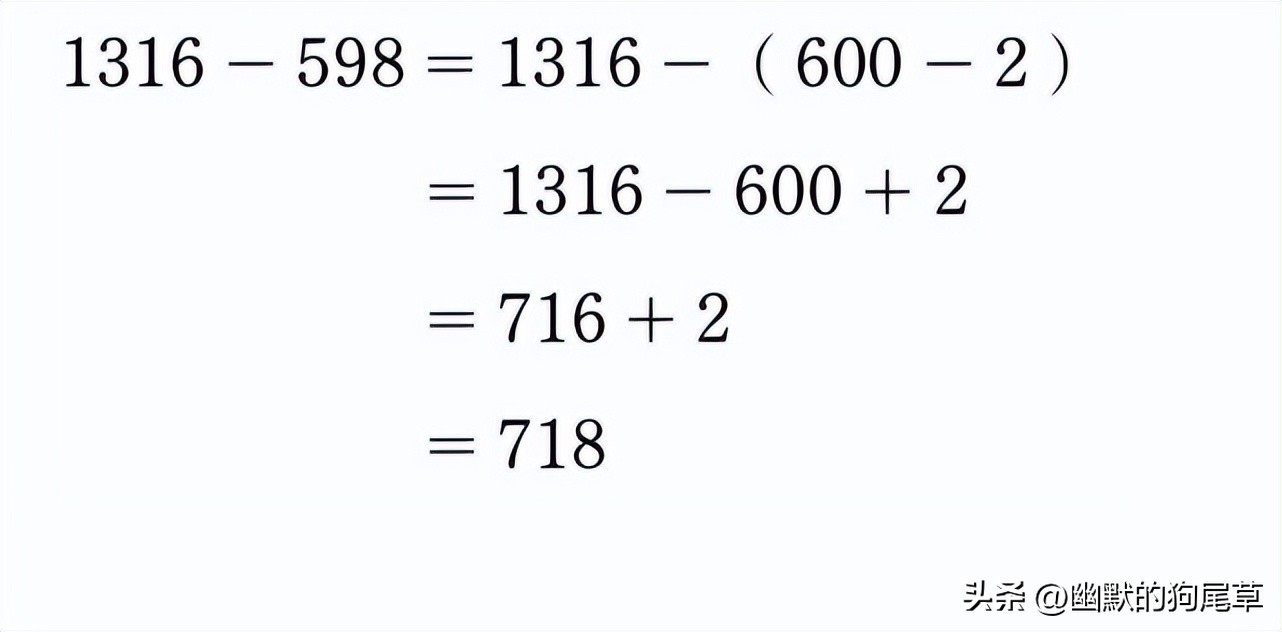
这就是我们的算式。

所以“故意多减去一点”的计算，实际上就是将（）中多减的数字表示为-（x-y）的形式，去掉括号就变成了-x+y。

多运用“多减去一点”的方法，在练习中自然而然就能理解它的 原理了。

06 如何计算1012-676——减法与距离（“爬山时的减法”）

加法与减法是相逆的。因此，在思考“1012减去多少等于676”时，只需反过来思考，“676加多少等于1012？”

请看图。

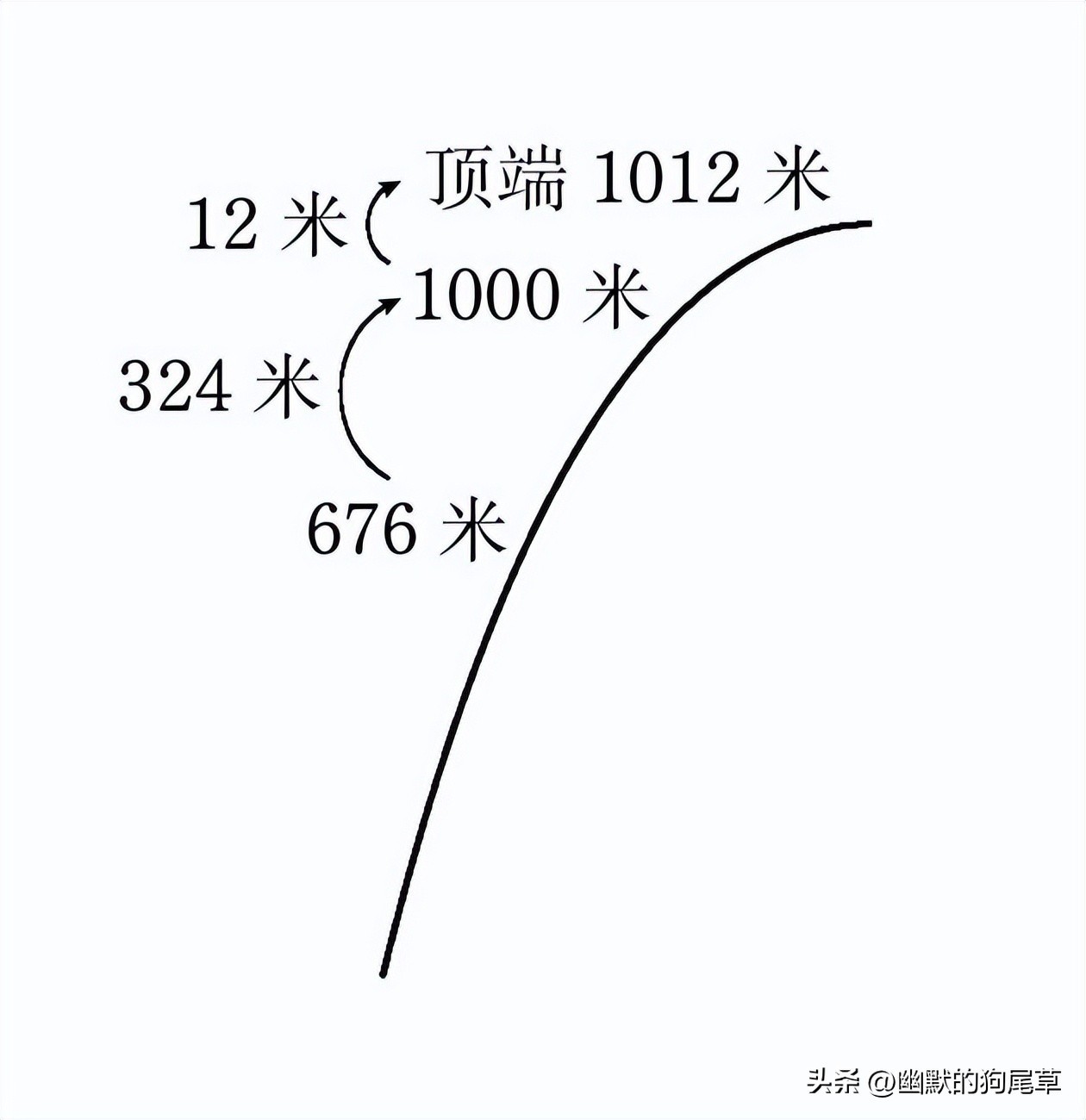
如果我们从图上676米高的地方开始向上爬，爬多少米可以到达1012米呢？

用上一节的方法，从676米到1000米需要324米。最后还剩12米，即676米到顶端的高度差为336米。

即1012-676=336米。

换一种方式来看，我们先在下图的横线上用点标出676和1012的位置，题目就变成了计算从676到1012之间的距离。

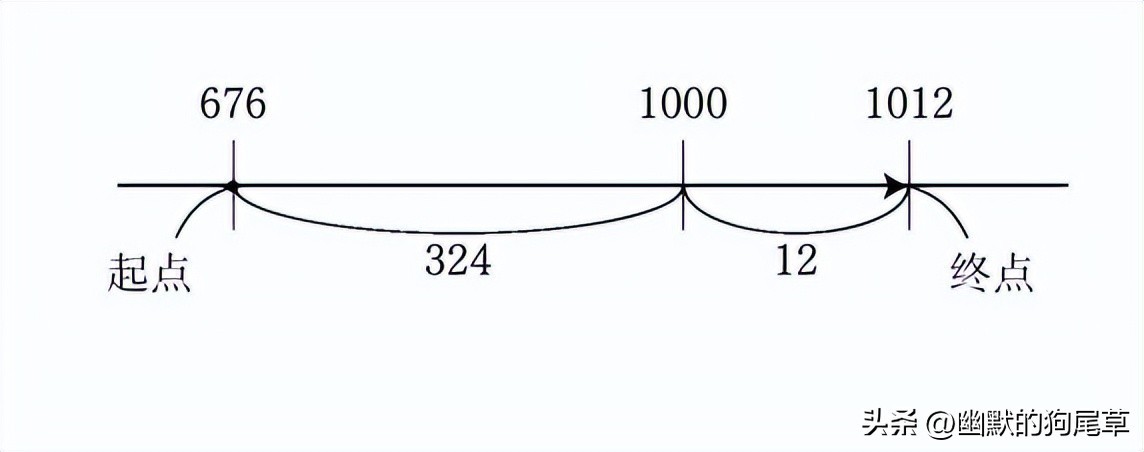
因此在经过1000的时候，我们就可以将这个易于计算的整数单独 标记。

像这样，减法的概念和距离的概念就紧密结合在了一起。我们也可以将上图所示的676作为出发点（起点），将1012作为终点。

如果掌握了这种方法，等到高中阶段学习向量的时候，理解起来就非常简单了。

07 如何计算827-339——“强弱减法”

假设A有827颗弹珠，B有339颗弹珠，请问A比B多多少颗弹珠呢？

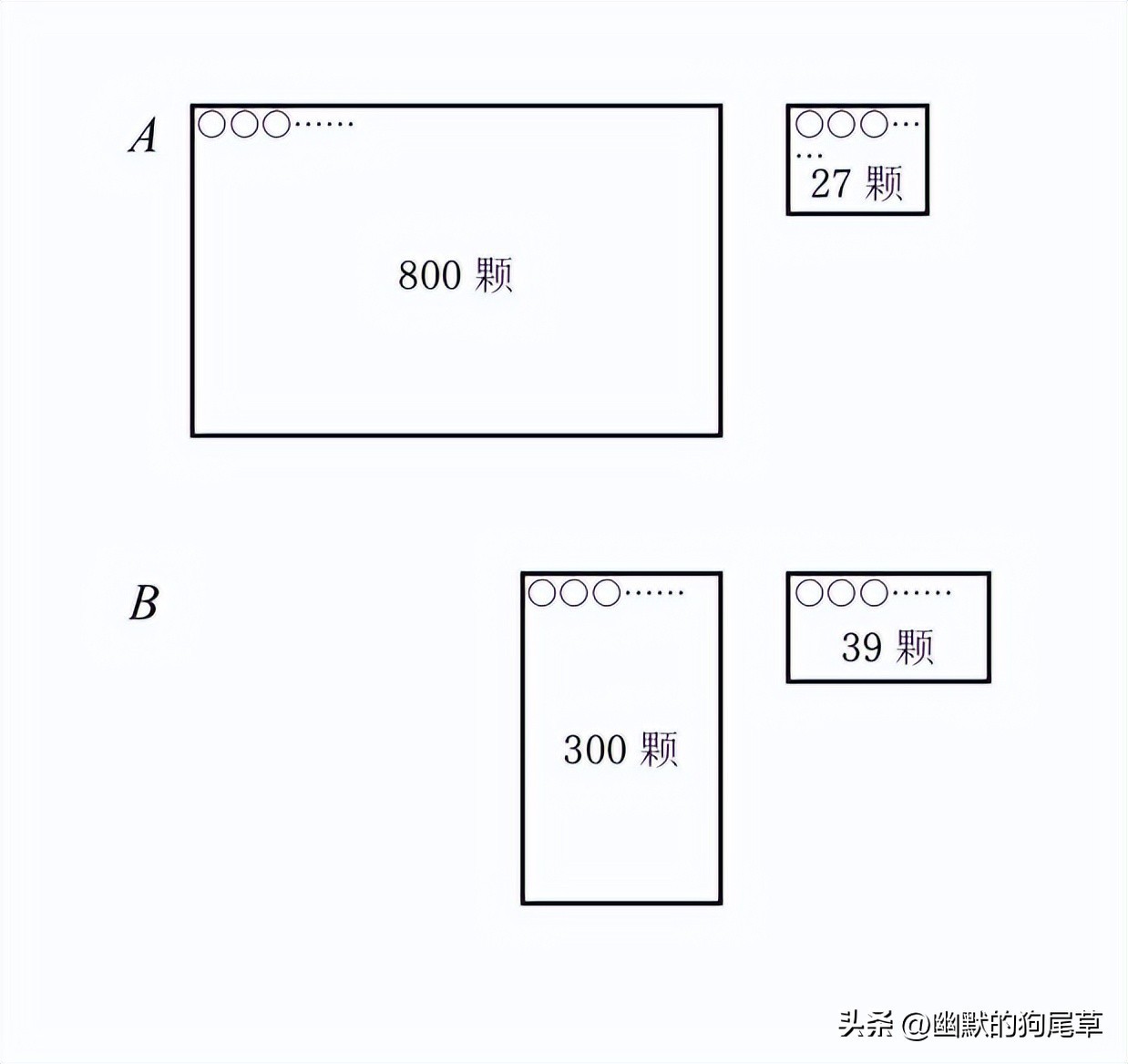
排好之后，我们可以先比较800颗和300颗孰多孰少。

如果每个人都将小弹珠一颗一颗拿掉，拿掉第300颗以后B就没有了，而A还剩下500颗。这时A就会想：“太棒啦，我赢了500颗。”

接下来，将27颗和39颗做比较，当两个人各拿掉27颗以后A就没有了，而这回B多了12颗。

A想：“哎呀，这次我输了12颗”。

最后，将500颗和12颗比较，当A和B各拿掉12颗以后，A还剩488颗弹珠，而这时，B已经没有了。

我们来总结一下。

在比较A的827和B的339孰多孰少之前，我们如果先看百位就可以发现，A比B多了500。而看到后两位时，则可以发现B比A多了12。所以在最终对决时，将500和12相比，就可以看到，500比12多了488。

除了像上面这样对比外，我们还可以用如下算式表示：

在上面的式子中，我们是将27转化成-（×××-27），熟练之后，这种做题技巧就能自然而然地加以使用。

其实，这个计算方法与“依次减去相同数字”的方法类似，我们可以像下面这样表示出来：

827和339→（依次减去300）527和39

→（依次减去27）500和12

最后500-12=488。

08 如何计算364-（273-136）——排列·组合（凑整）

加减法速算秘籍！组合式计算，让难题变简单！

当加减法计算项超过3个时，你是否觉得计算变得吃力又繁琐？别担心，我们有一个超实用的秘籍——组合式计算！

秘籍揭秘：

在计算只含有加减法的算式时，观察各项的顺序和组合，找出最简单的组合进行计算，是关键！

实例演示：

356+487+644直接按顺序算？太累！换个思路，356+644=1000，再+487=1487，轻松搞定！364-（273-136）遵守规则先算括号？太烦！去掉括号，364+136=500，再-273=227，简单快捷！672-183-272依次相减？太慢！先算672-272=400，再-183=217，效率翻倍！672-183-117类似上题，但更巧妙！把183和117凑一起，672-（183+117）=672-300=372，一秒出结果！

秘籍核心：

观察：细心观察各项，找出能凑成整数的组合。组合：将能凑成整数的项组合在一起计算。简化：通过组合计算，简化计算过程，提高计算速度。

掌握了组合式计算秘籍，加减法计算再也不是难题！快来试试吧，让你的计算速度飞起来！

09 如何计算8.3-0.492——可以瞬间完成的小数减法

小数加减法，心算也能轻松驾驭！

在十进制的世界里，小数计算同样遵循着基本的法则。但别担心，即使面对小数，我们也能用心算轻松搞定！

你是否也曾被小数计算难倒？看看下面的题目，你能迅速给出答案吗？

10-0.04=？3.5-1.51=？

掌握方法，小数计算不再难！

对于第1题，你可以想象成1000-4，算好后调整小数点，得出9.96。或者，你也可以先算出0.04到1还需0.96，再从10中减去这1（即减去10中的9，剩下1），再加上剩下的0.96，答案同样是9.96！对于第2题，试试“强弱减法”吧！前后项都减去1.5，得到2-0.01，轻松得出1.99！

掌握了这些方法，连8.3-0.492这样的题目也变得简单起来！

8比0多了8，0.492比0.3多了0.192，所以只需计算8-0.192，答案就是7.808！

再来看个例子，1.02-0.486：

用“爬山时的减法”：从0.486爬到1需要0.514，再加上多出的0.02，答案就是0.534！或者用“强弱减法”：直接计算1-0.466（因为0.486近似为0.466，方便计算），答案同样是0.534！

来个小测试，看看你是否掌握了这些技巧：

100-11.001=？

答案揭晓：88.999！

如果你答对了，那就继续挑战后面的练习题吧！相信你一定能成为小数加减法的心算高手！

10 如何计算38×7——两位数×一位数

在乘法心算中，最重要的法则是“乘法分配律”。

以38×7为例，我们进行如下计算。

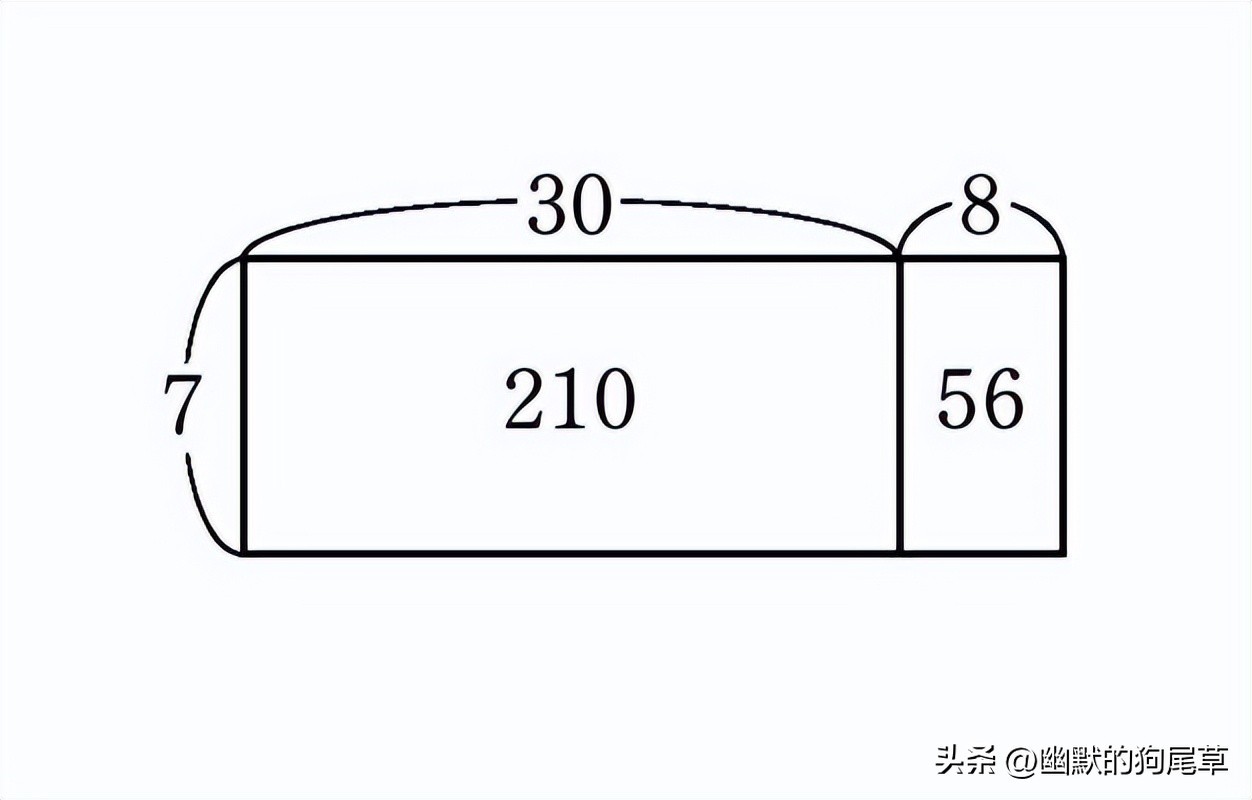
可以参考上方的面积图来看左侧的计算流程。

我们可以想象一下，假设有7块豆饼，每一块豆饼上都有38颗小豆子，那么，当我们计算所有豆饼上小豆子的总数时：

7个30颗小豆子的豆饼，7个8颗小豆子的豆饼

可以像上面这样分开计算之后再相加，就可以得出答案。

心算本题时，我们需要在3×7=21的后面添0，并将得到的210记在脑中，在最后得出7×8=56后，将二者对接。

也就是说，计算一共分为两个阶段：将第一阶段的答案记住，与此同时进行第二阶段的计算。

对于刚开始学习的朋友来说，这可能需要花一些时间来适应，但当我们掌握了这种方法，就会慢慢发现它的有趣和实用之处。

我们可以先试着挑战简单一些的题目，如12×7，之后再慢慢挑战 难题。

除此之外，还有以下解题思路，我们可以看情况选择合适的方法：

（1）乘以9（看作10减1）。

例：17×9=17×（10-1）=170-17=153

28×9=28×（10-1）=280-28=252

（2）乘以39 （看作40减1）。

例：39×7=（40-1）×7=280-7=273

49×8=（50-1）×8=400-8=392

11 如何计算395÷2——一半是多少（1）

除法心算大揭秘！轻松掌握除以2的秘诀！

除以2，听起来简单吧？求某数的一半，这可是数学里的基础操作哦！偶数除以2，小菜一碟；奇数除以2，虽然有点挑战，但别担心，我们有妙招！

想象一下，8除以2等于4，轻松搞定！但7除以2呢？得到3.5，嗯，有点小数的感觉了。

现在，让我们来挑战一下395÷2这个题目！其实，我们的方法和笔算差不多，但更快捷哦！

先看百位：3除以2得1，余1。我们把1看作100的“头”，然后留下那个1，备用。再看十位：把刚才余下的1和9加在一起，变成19。19除以2得9，又余1。这次，我们把9看作90的“头”，1再留下来。最后看个位：把十位余下的1和5加在一起，变成15。15除以2得7.5，搞定！

所以，395÷2的答案就是197.5！

仔细观察一下，我们其实一直在做“从大至小依次除以2，遇奇数余1留到下一步”的工作。这个技巧，对于两位数的奇数，特别是11、13、15、17、19这些数字，简直不要太好用！

习惯了这个方法，遇到更大的数字，比如75839÷2，也不在话下！

判断：要不要余1留到下一步？迅速除以2：依次把7、15、18、3、19这些“组合”除以2，得到3、7、9、1、9、5。

在脑子里迅速把这些数字排好队，“三、七、九、一、九、五”，别忘了小数点，答案就是37919.5！

怎么样，是不是觉得除以2也没那么难了？快来试试吧，你也能成为除法心算小达人！

12 如何计算54×15——一半是多少（2）

乘法心算新技巧！轻松求“一半”的奥秘！

在乘法世界里，求某数的一半，就是“乘以0.5”，这么简单，你get了吗？

想象一下，54×0.5，就是把54分成两半，答案就是27！或者，你也可以先让54乘以5，再把小数点向左挪一位，答案还是27！

让我们来看看几个实例，感受一下这个技巧的魅力吧！

3.4×1.51.5倍就是“自己加自己的一半”，所以3.4+1.7=5.1！54×15这就是把54的10倍和5倍加起来，540+270=810！42×0.15先算42×1.5，再挪小数点，42+21=63，小数点左移一位，答案就是6.3！23×0.35先算23×3.5，再挪小数点，23×3=69，23的一半是11.5，加起来80.5，小数点左移一位，答案就是8.05！54×0.55乘以0.55就是“一半加上小数点前挪一位的一半”，所以27+2.7=29.7！或者看作54×55，先算54×5=270，进位成2700，再加起来2970，小数点左移两位，答案还是29.7！

心算，就是灵活运用各种方法，让计算变得简单又有趣！快来试试这些技巧，成为乘法心算小达人吧！

13 如何计算13×73——两位数×两位数（心算明星题）

两位数×两位数可以说是心算中的明星题。

我们甚至可以说，这项计算的快慢直接关系到心算能力的高低。

那么，我们该如何计算13×73呢？

请看右图。

这是一个宽13、长73的长方形，它的面积大小表示13×73的大小。

看图即可发现，a的面积为730，b的面积为210，c的面积为9。将所有和相加，得到949的答案。

如下，是老师此时的思路：

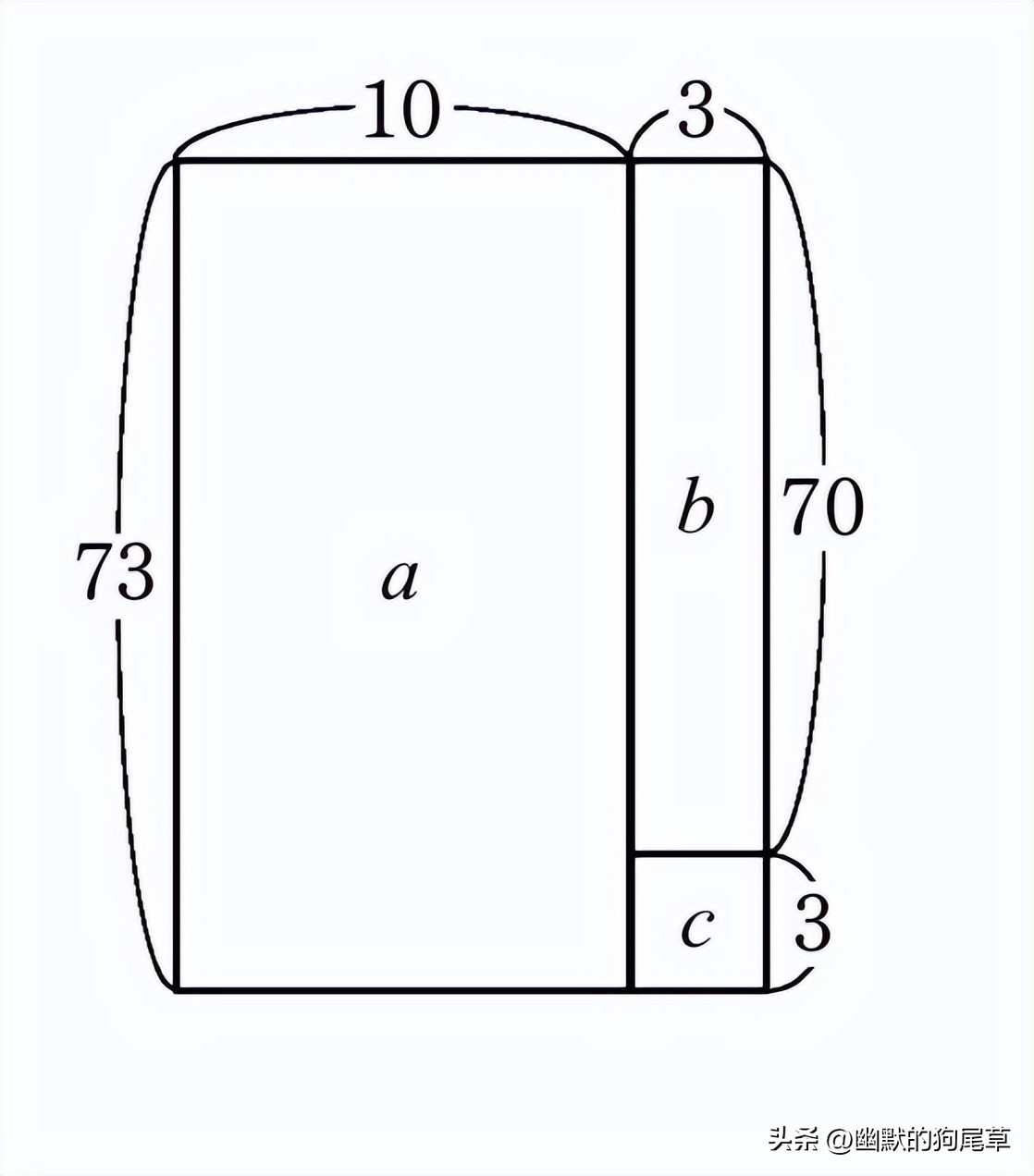
① 有10个73，所以先得到730。

② 将730记在脑中进行下一步计算。

③ 接下来有3个73。

④ 可以立刻计算出73×3得219的人不用看这一步。

如果不能立刻算出，我们可以先计算3×70得210，记在脑中，再计算3×3得9，二者相加得到219。

⑤ 最后在脑中计算730+219，得到949。

为了解释得更清楚些，我特意将过程写得长了一些，实际做起来速度是非常快的。

那么，我们该如何计算47×83呢？

这道题难一些。50个83得4150，然后减去3个83即249得3901（可以先减250再加1）。

做类似题型时，最重要的是要找到易于计算的组合。上面的例子中，如果将47×83看作47×80+47×3，计算起来相对简单，但如果分解成83×40和83×7，计算起来就相对复杂了。

因此，在进行复杂的心算时，能否牢记数字、找到最佳分解法是非常关键的。

14 如何计算75×32——分解质因数

做加法时，我们可以将算式746+38看作746+30+8，即将38分解成30和8，分两个阶段进行计算。

同样的，一些乘法题我们也可以通过分成两个阶段来简化计算。

以标题为例：

75=3×5×5    32=2×2×2×2×2

将这些数全部相乘，即：

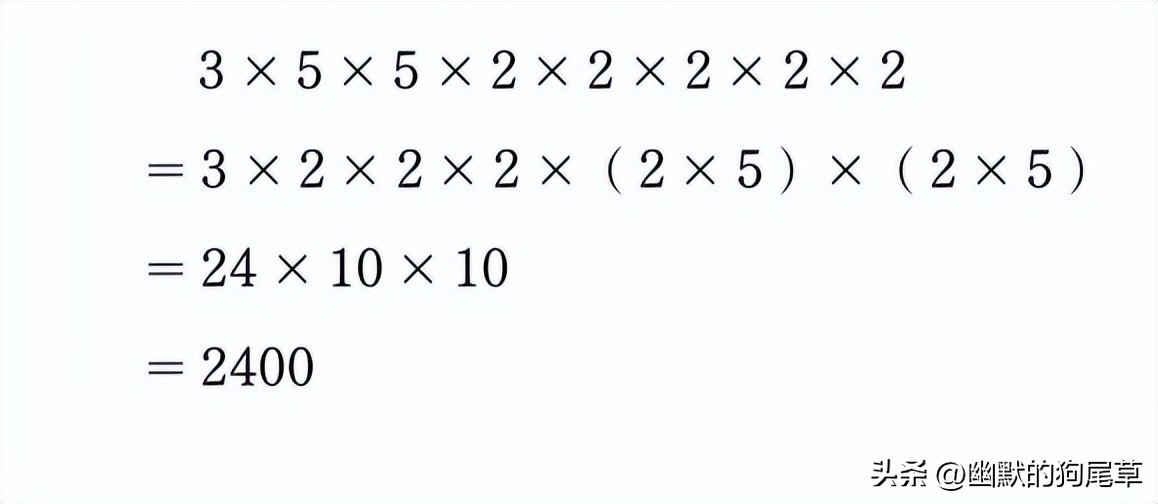
但是在这道题中，如果我们一股脑儿将75和32因素分解（分解为各因素的乘积），效率反而会有所下降。

那么，我们应该怎么做呢？

（1）将原式分解为75×2×16，而后变为150×16，进而变为150×2×8，计算300×8得2400。

（2）熟练的同学可以直接记住75×4得300，那么75×4×8=300×8=2400。

（3）我们基本上都知道25×4=100，那么75=3×25，32=4×8，3×8=24，后面再添两个0即得2400。

熟练的同学可以使用上述方法迅速得出答案。

这些方法多用于计算整数×整数，尤其是一边末位为5，另一边为偶数的题目。

本质上是运用了5×2=10（可以得到整数的计算）。

比如，26×35可以看作先求26的一半，再求35的2倍，即13×70，从而迅速得出910的答案。

同时，在计算此题目的过程中，我们会频繁接触到如25×4=100，75×4=300，125×8=1000等式子，可以记住这些答案，进而直接运用在计算中。

15 如何计算3.5÷140——除法即分数

16 如何计算37÷0.2——小数和分数的相互转化（1）

在计算÷0.5、÷0.2、÷0.25这样的式子时，我们不必直接除，可以先做如下转化：

÷0.5→×2  ÷0.2→×5  ÷0.25→×4

这样计算就简单了许多。

我们再将小数转换为分数：

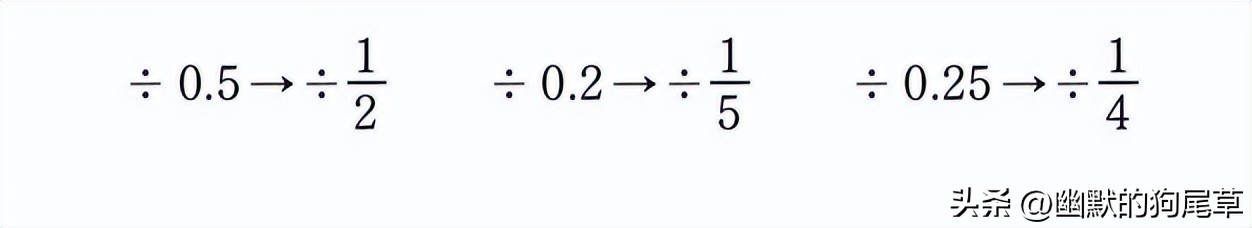
对比两种转化方式我们可以发现一个规律，即“除以分数相当于乘以它的倒数”。例如在计算5÷0.25时：

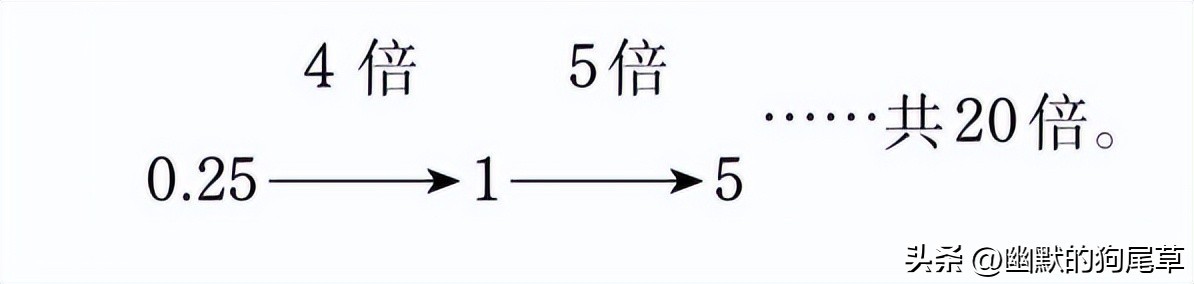
我们可以迅速找到这种转化的感觉。

因此，以本节标题37÷0.2为例，我们可以立刻将37乘以5得出185的答案。

同样，解3.7÷0.5时，将3.7乘以2即得答案7.4。

解5.26÷0.25时，将5.26乘以4即得答案21.04（计算5.26×4时，我们可以先计算4×5=20，而后0.25的4倍得1，最后0.01乘以4得0.04）。

这种将除数转化为分数后再进行计算的方法，对于上述这些特殊的数字运算非常有效，但若遇到如下（1）～（3）的情况，这种方法。并非全部适用，我们应该尝试活用多种方法。例如：

（1）在做2.1÷0.35时，可以将0.35乘以2得0.7，再乘以3得2.1，答案即为2×3得6。

（2）在做64.05÷0.21时，可以先忽略1.05，将0.21乘以300得63。余下的1.05正常除以0.21即得5。最后合起来得305。

（3）在做0.39÷0.65时，可以先同乘以100得39÷65，再同时“约分”13，得3÷5=0.6。这种方法比较迅速。

如果拿到题目不加以辨别就直接转化为分数，很可能会影响做题的效率。

17 如何计算21÷3.75——小数和分数的相互转化（2）